Introduction

This is an analysis of Codility - Silicium 2014 Challenge.

• The problem is, finding the k-th largest piece of cake after cutting a big cake with straight cuts.
• The longest edge of a cake piece is 10000.
• Time bound is O(N * log(N + X + Y)), where N is the number of cuts, X and Y are largest size of the cake.
• Space bound is O(N).

Analysis

In order to find the k-th element is an array of set of elements, we can always do binary search. Find a middle elements, calculate the rank, do partition if needed, recursively.

• First, we calculate length of each edges, the sort them by their length.
• Then do a traditional binary search.

The interesting thing is that, for calculating the rank of an element in such 2-d array, we have to calculate all elements, then sort them. This costs at least O(N²) time.

But in this problem, after we sort edges in x and y, we can do rank calculation in O(N) time, as implemented in fastPartition method.

(Hint: after we sort the edges, we can ensure that elements in left-bottom are always equal or smaller than elements in right-top. We can search from left-top to right-bottom, following the red arrow, in O(N) time)

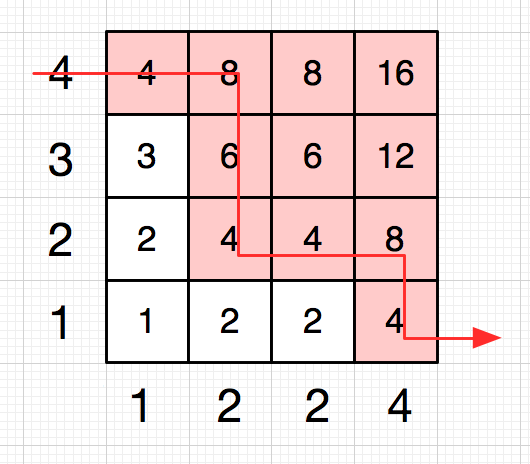
For example, let $x = (1, 2, 2, 4), y = (1, 2, 3, 4)$. We need the rank of target ‘4’.

First, we need the start element at the left-most column. We just do a binary search on the left-most column, to find the element equal or larger than target in left-most column. Then we know we should start from column 1, row 4, which is exactly, ‘4’. (Step 1).

Then we move to next line in the right. We need go up to down, until find an element is smaller than target. Now we arrive at column 2, row 2, which is also ‘4’. (Step 2)

And repeat step 2, until the right-most column. (Step 2)

Because elements in left-bottom(which background) are always equal or smaller than elements in right-top(red background), we can calculate target’s rank by add up number of white elements, for each column. (Step 3)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79

int N;
int[] largerEqualList;

private int fastPartition(int target, int[] x, int[] y) {

    // Step 1
    // find the element equal or larger than target in left-most column
    int nx = 0, ny = 0;
    int low = 0;
    int high = N;
    while (low <= high && low < N) {
        int mid = (low + high) / 2;
        if (x[nx] * y[mid] < target) {
            low = mid + 1;
        } else {
            high = mid - 1;
        }
    }
    ny = low;

    largerEqualList[nx] = ny;

    // Step 2
    // search elements' index by red arrow mentioned above
    while (++nx < N) {
        while (ny - 1 >= 0 && x[nx] * y[ny - 1] >= target) {
            --ny;
        }
        largerEqualList[nx] = ny;
    }

    // Step 3
    // get the rank of target
    int rank = 0;
    for (int i = 0; i < N; i++) {
        rank += N - largerEqualList[i];
    }

    return rank;
}

public int solution(int X, int Y, int K, int [] A, int [] B) {

    int [] x = new int[A.length + 1];
    int [] y = new int[A.length + 1];

    for (int i = 0; i < A.length + 1; i++) {
        x[i] = (i < A.length ? A[i] : X) - (i > 0 ? A[i - 1] : 0);
    }

    for (int i = 0; i < A.length + 1; i++) {
        y[i] = (i < A.length ? B[i] : Y) - (i > 0 ? B[i - 1] : 0);
    }

    Arrays.sort(x);
    Arrays.sort(y);

    N = x.length;

    largerEqualList = new int[N];

    int low = x[0] * y[0];
    int high = x[N - 1] * y[N - 1];
    int rank = K;

    // binary search
    while (low <= high) {
        int mid = (low + high) / 2;
        int crank = fastPartition(mid, x, y);

        if (crank >= rank) {
            low = mid + 1;
        } else if (crank < rank) {
            high = mid - 1;
        }
    }

    return high;
}

Each fastPartition cost O(N) time, and we do log(10000 * 10000) times. So the total time is O(N * log(10000 * 10000). There is no X and Y occurs.
Note that even a traditional O(N²) time partition could pass system test. :)